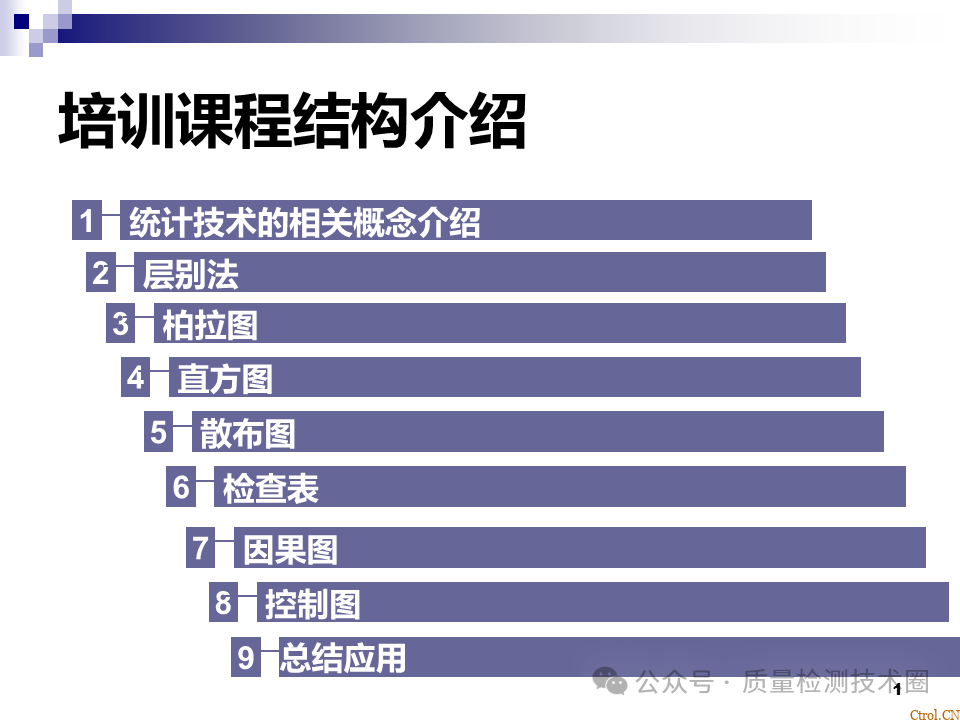
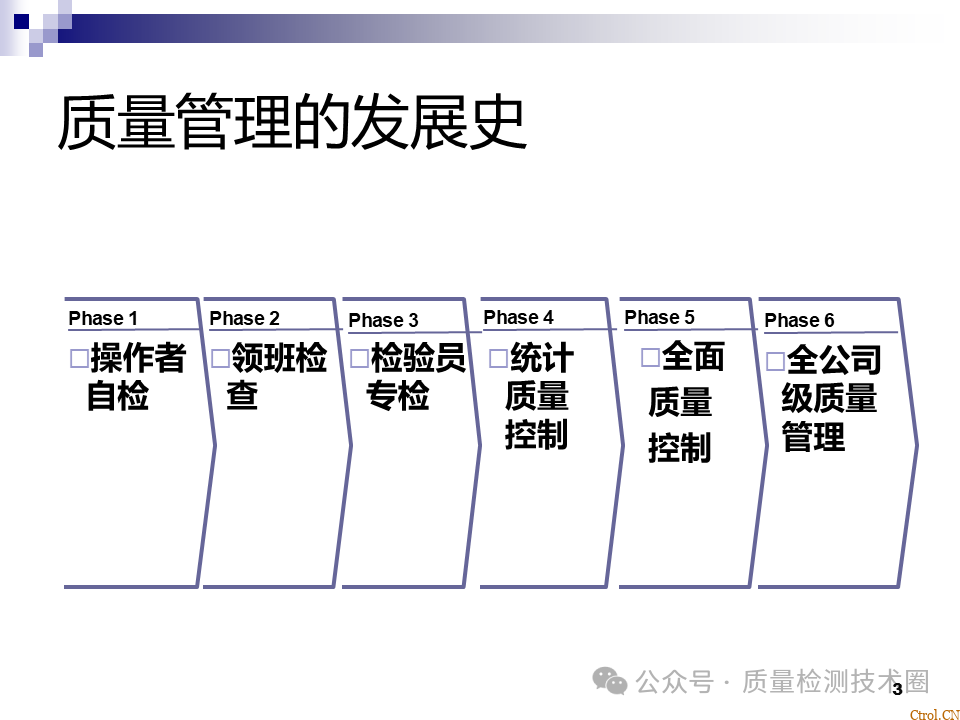
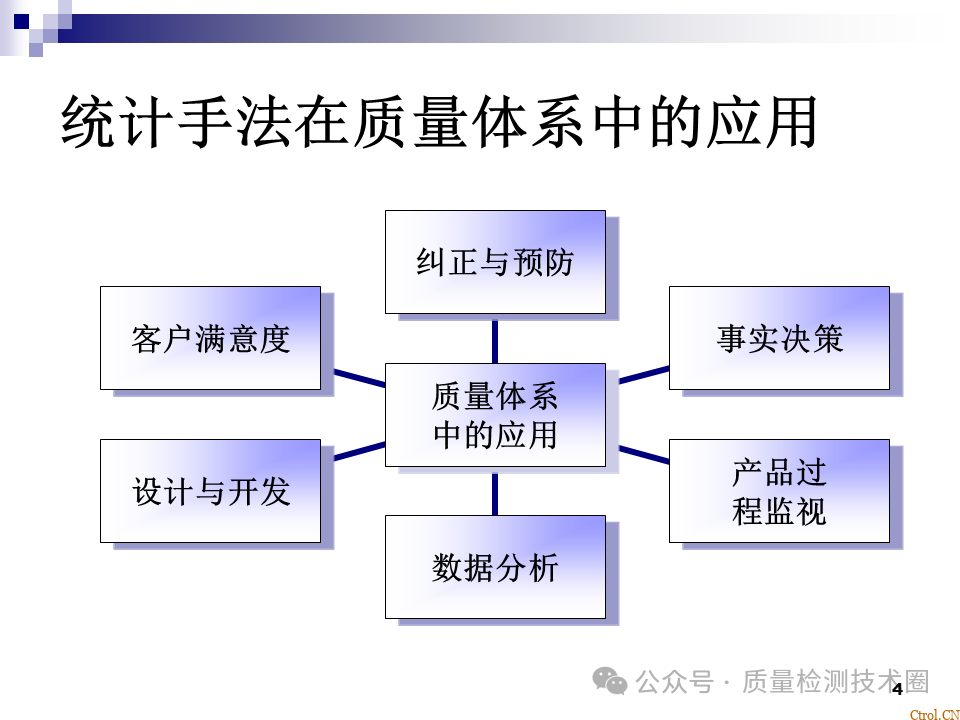
共计 2206 个字符,预计需要花费 6 分钟才能阅读完成。
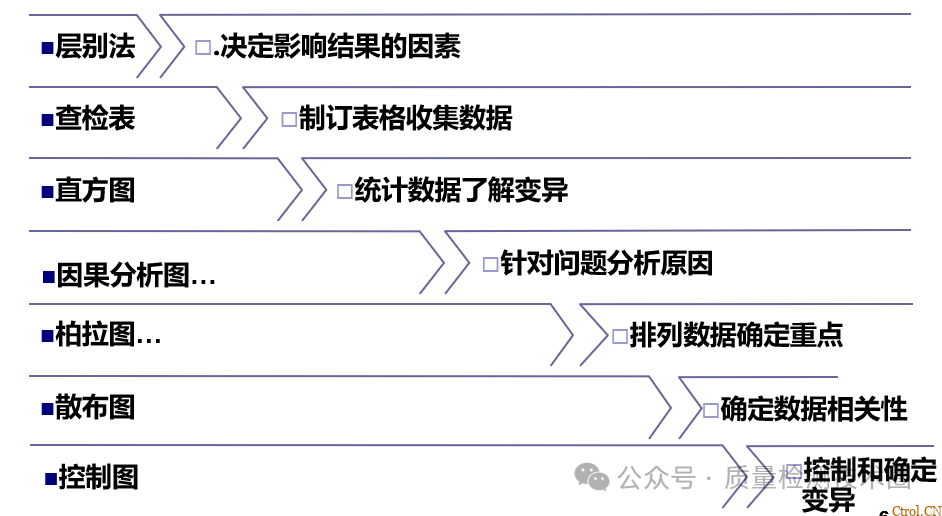
一、检查表(Check Sheet)
- 确定检查的项目;
- 确定检查的频度;
- 确定检查的人员;
- 制定检查表;
- 依检查表项目进行检查并记录;
- 对检查出的问题要求责任单位及时改善;
- 检查人员在规定的时间内对改善效果进行确认;
-
定期总结,持续改进。
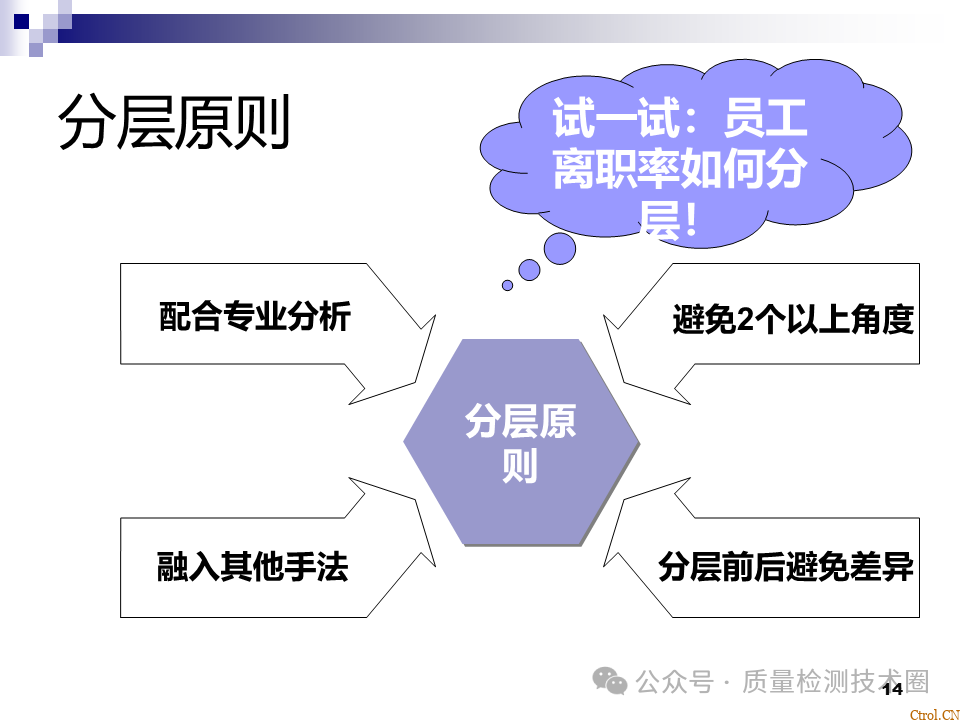
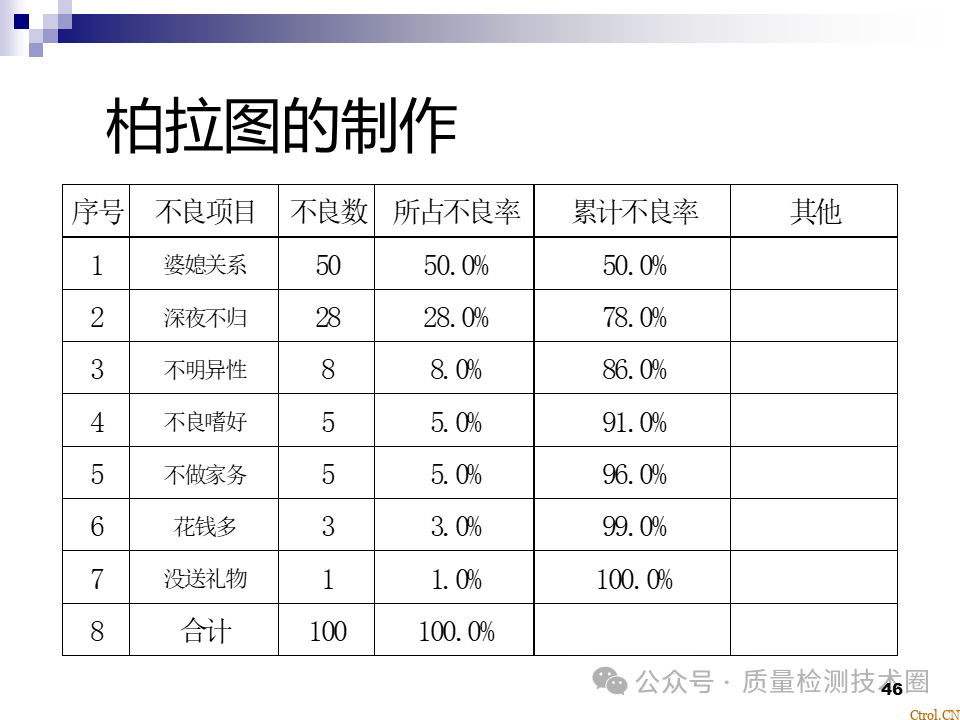
- 确定研究的主题;
- 制作表格并收集数据;
- 将收集的数据进行层别;
-
比较分析,对这些数据进行分析,找出其内在的原因,确定改善项目。
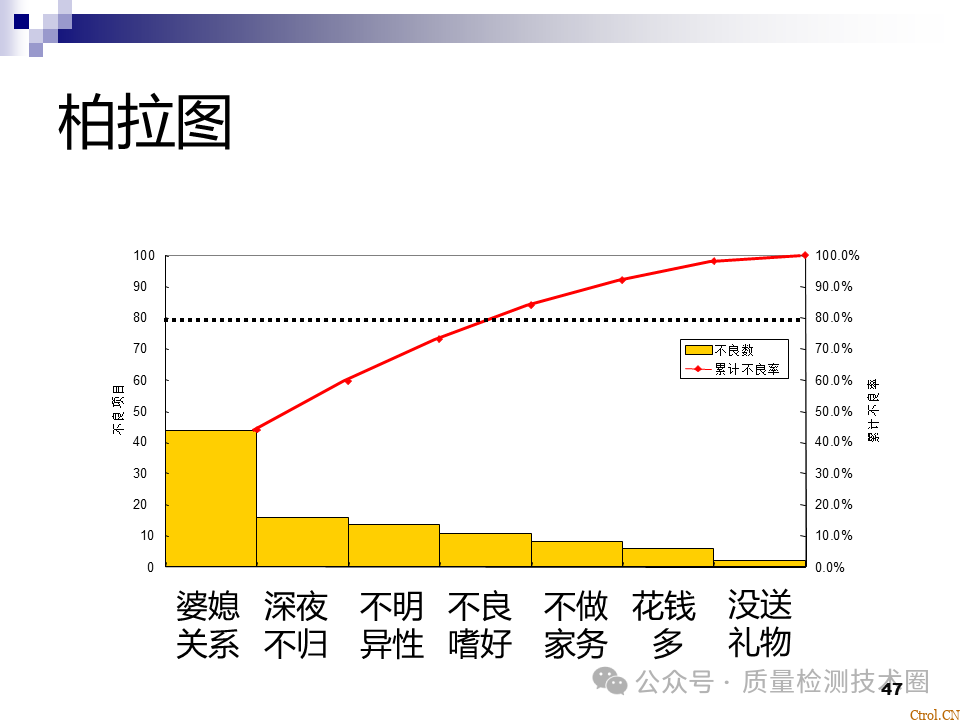
- 分析现象用柏拉图:与不良结果有关,用来发现主要问题;
-
分析原因用柏拉图:与过程因素有关,用来发现主要问题。
- 降低不良的依据;
- 决定改善目标,找出问题点;
-
确认改善的效果。
- 柏拉图要留存,把改善前与改善后的柏拉图排在一起,可以评估出改善效果;
- 分析柏拉图只要抓住前面的2~3项即可;
- 柏拉图的分类项目不要定得太少,5~9项较合适,如果分类项目太多,超过9项,可划入其它,如果分类项目太少,少于4项,做柏拉图无实际意义;
- 作成的柏拉图如果发现各项目分配比例差不多时,柏拉图就失去意义,应从其它角度收集数据再作分析;
-
柏拉图是管理改善的手段而非目的,如果数据项别已经清楚者,则无需浪费时间制作柏拉图。
- 追求原因型:在于追求问题的原因,并寻找其影响,以因果图表示结果(特性)与原因(要因)间的关系;
-
追求对策型:追求问题点如何防止、目标如何达成,并以因果图表示期望效果与对策的关系。
- 成立因果图分析小组;
- 确定问题点;
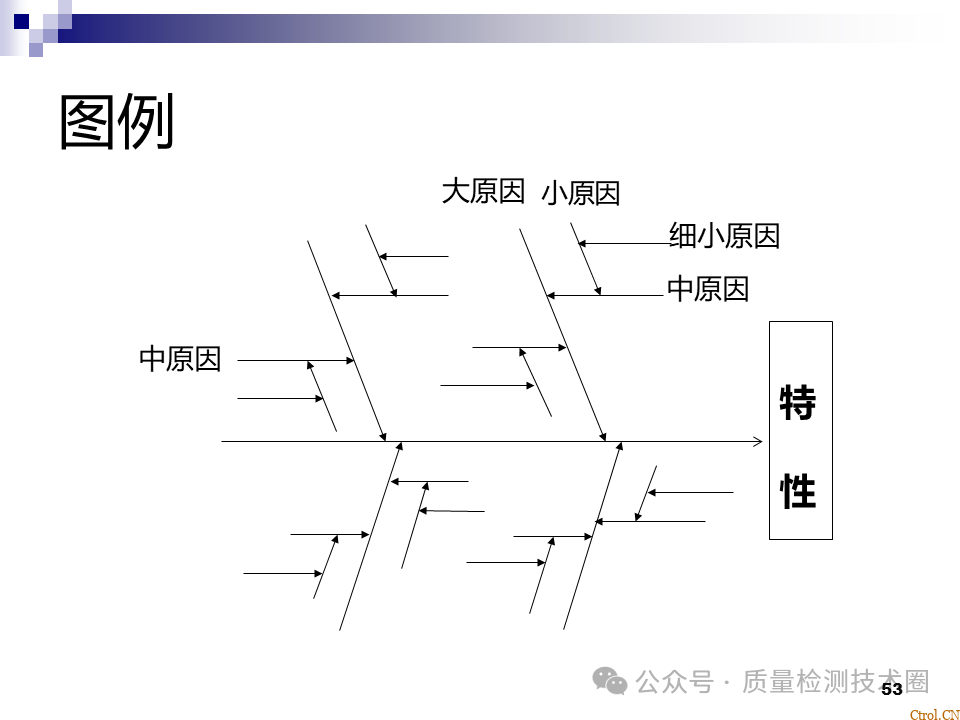
- 画出干线主骨、中骨、小骨及确定重大原因;
- 与会人员热烈讨论,依据重大原因进行分析,找到中原因或小原因,绘至因果图中;
- 因果图小组要形成共识,把最可能是问题根源的项目用红笔或特殊记号标识;
-
记入必要事项。
- 确定原因要集合全员的知识与经验,集思广益,以免疏漏;
- 原因解析愈细愈好,愈细则更能找出关键原因或解决问题的方法;
- 有多少品质特性,就要绘制多少张因果图;
- 因果图应以现场所发生的问题来考虑;
-
因果图绘制后,要形成共识再决定要因,并用红笔或特殊记号标出。
- 正相关:当变量X增大时,另一个变量Y也增大;
- 负相关:当变量X增大时,另一个变量Y却减小;
- 不相关:变量X(或Y)变化时,另一个变量并不改变;
-
曲线相关:变量X开始增大时,Y也随着增大,但达到某一值后,则当X值增大时,Y反而减小。
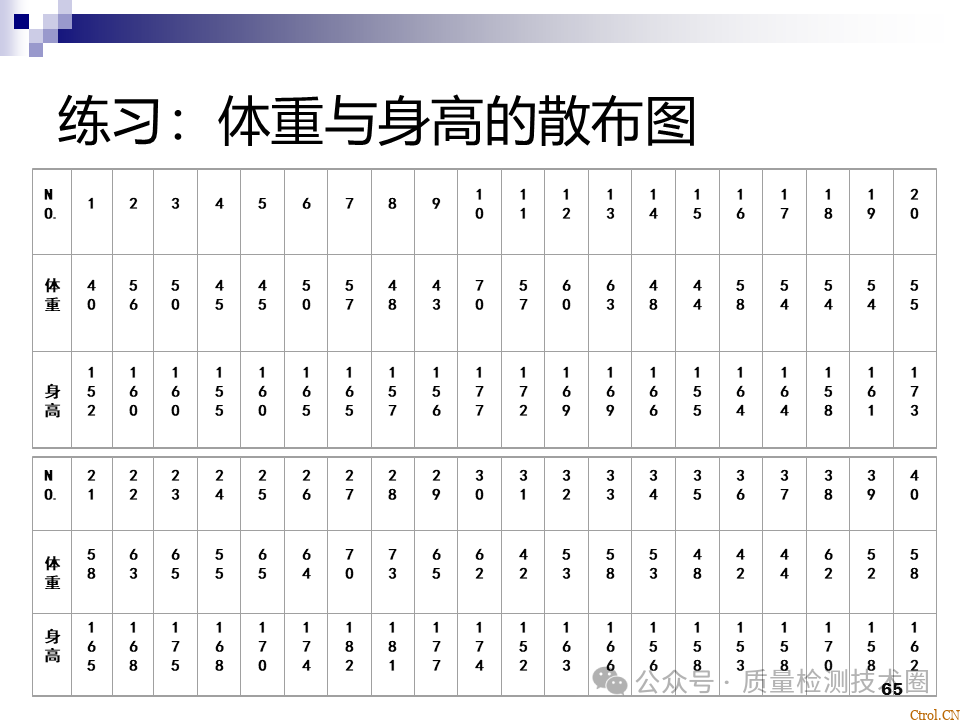
- 确定要调查的两个变量,收集相关的最新数据,至少30组以上;
- 找出两个变量的最大值与最小值,将两个变量描入X轴与Y轴;
- 将相应的两个变量,以点的形式标上坐标系;
- 计入图名、制作者、制作时间等项目;
-
判读散布图的相关性与相关程度。
- 两组变量的对应数至少在30组以上,最好50组至100组,数据太少时,容易造成误判;
- 通常横坐标用来表示原因或自变量,纵坐标表示效果或因变量;
-
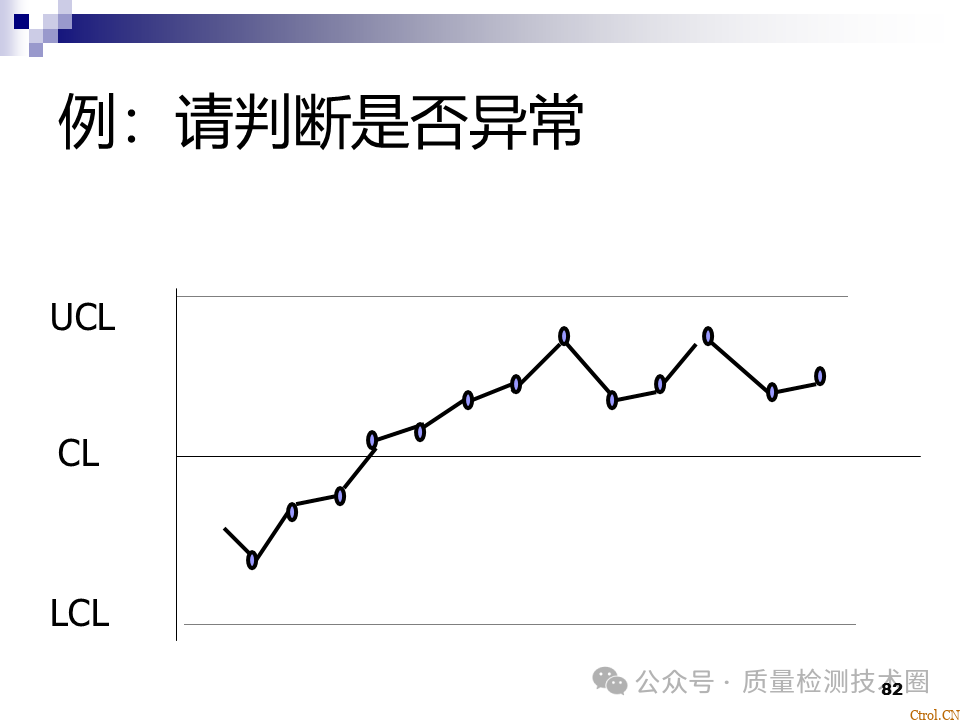
当有异常点出现时,应立即查找原因,而不能把异常点删除。
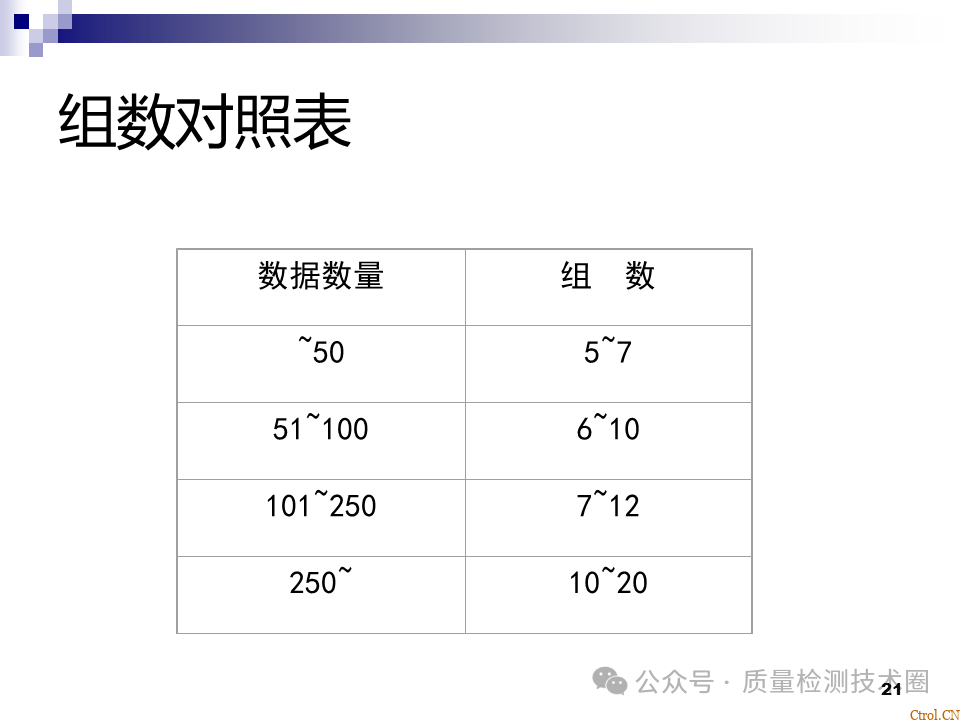
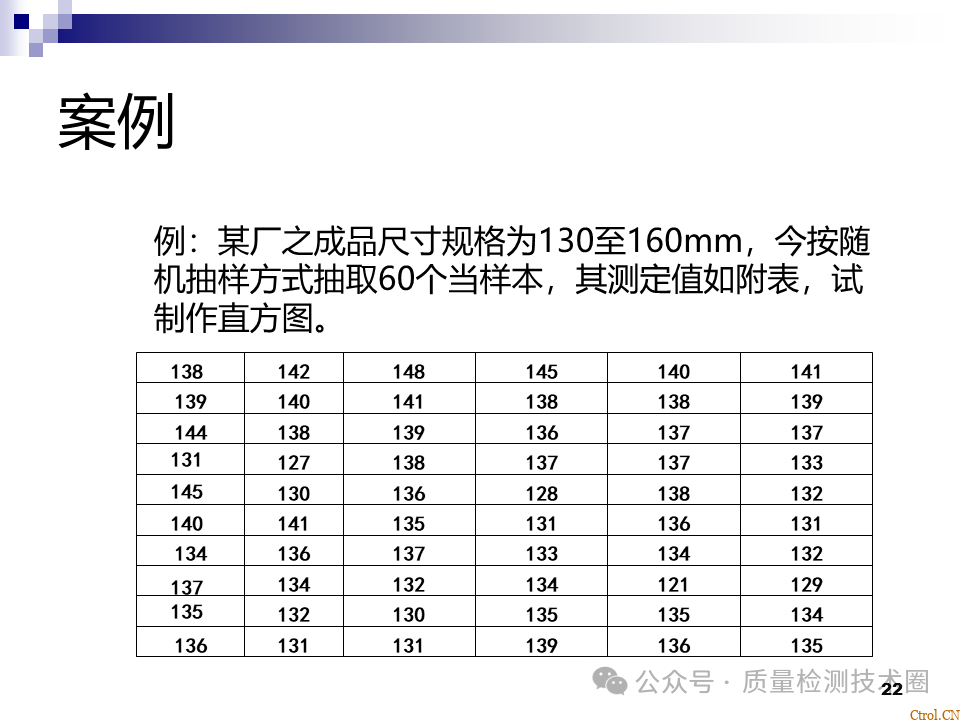
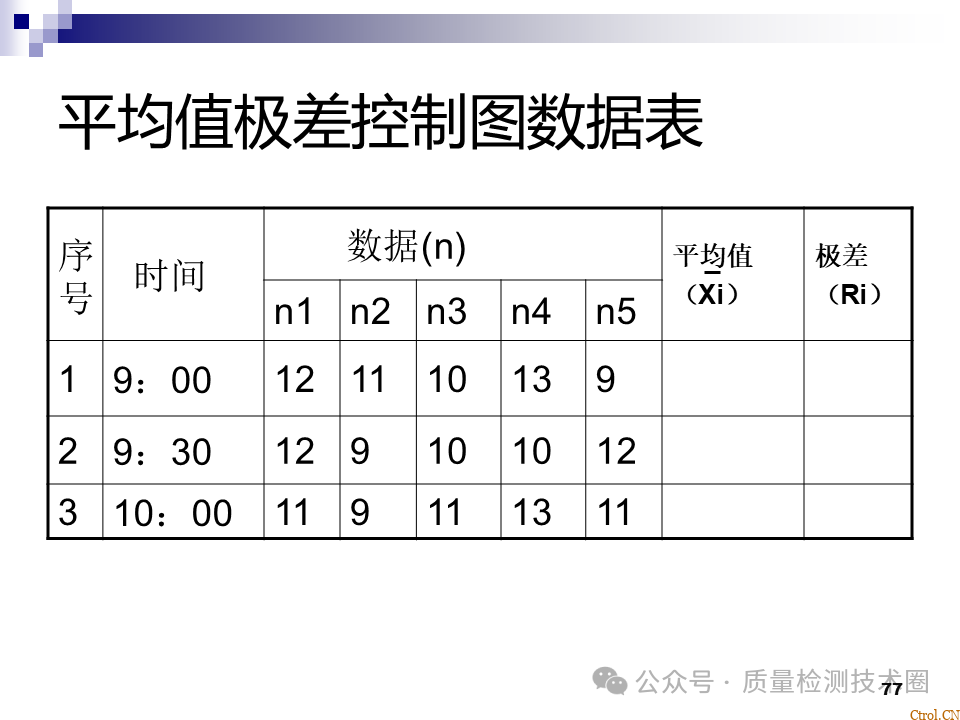
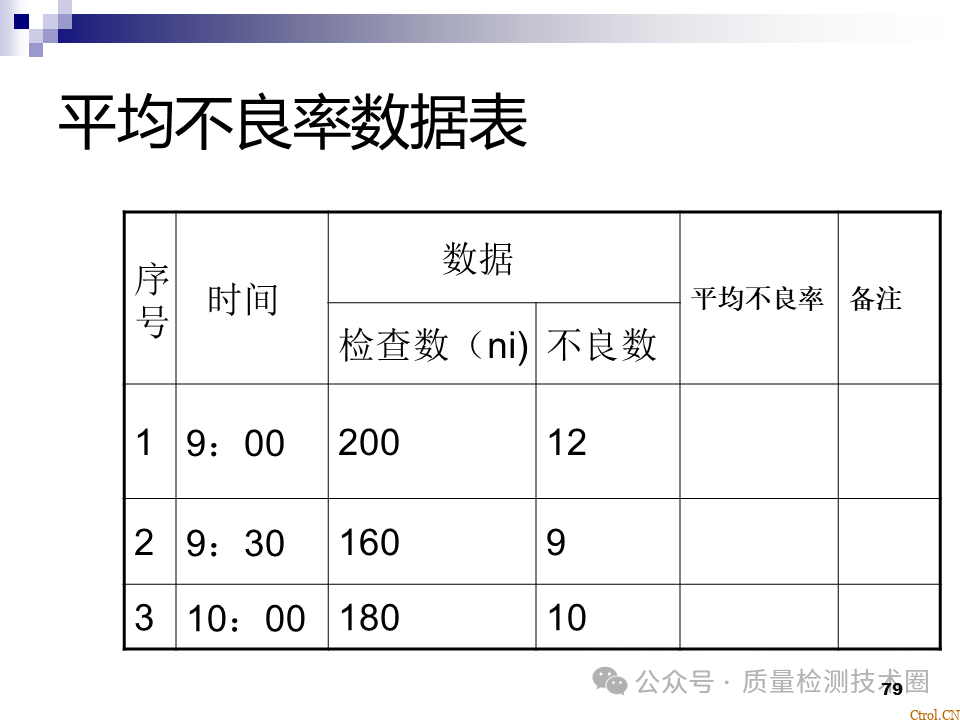
- 收集同一类型的数据;
- 计算极差(全距)R=Xmax-Xmin;
- 设定组数K:K=1+3.23logN;
- 确定测量最小单位;
- 计算组距h,组距h=极差R/组数K;
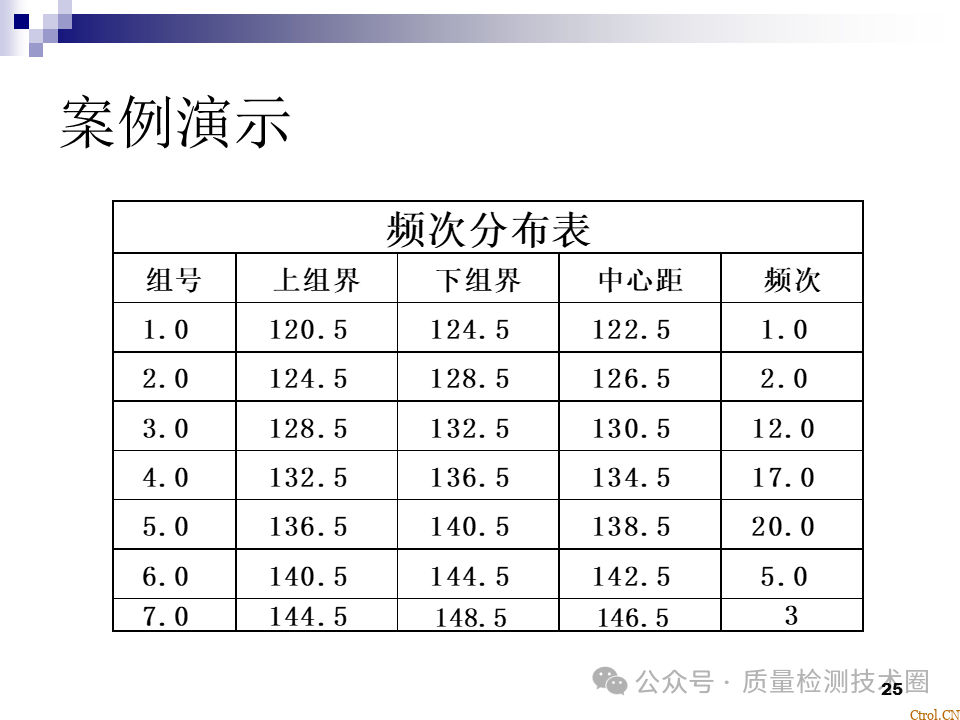
- 求出各组的上、下限值;
- 计算各组的中心值;
- 制作频数表;
-
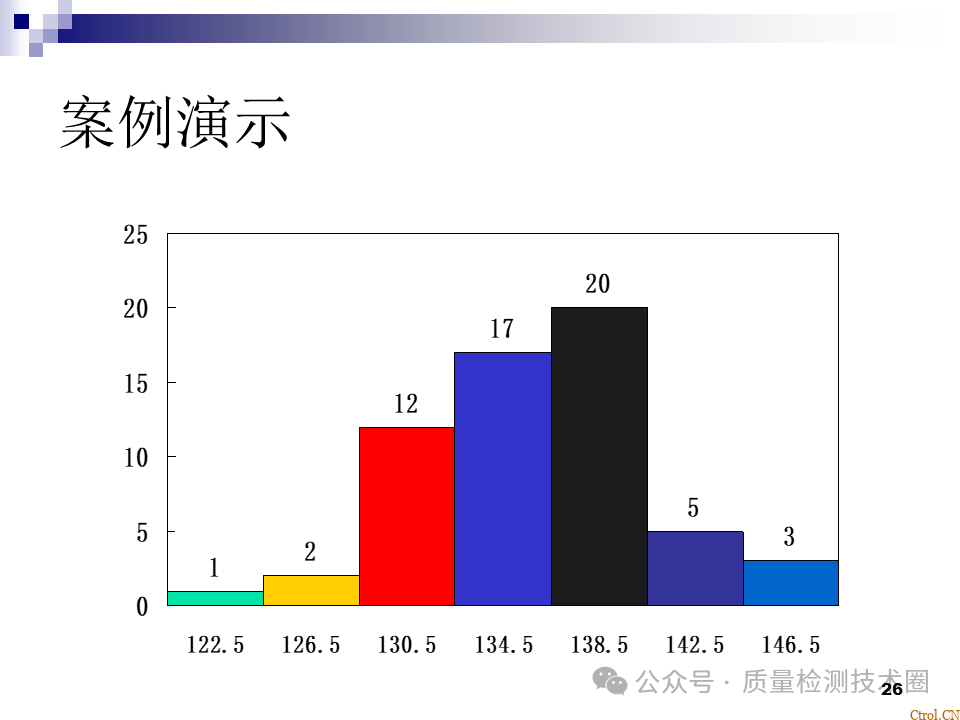
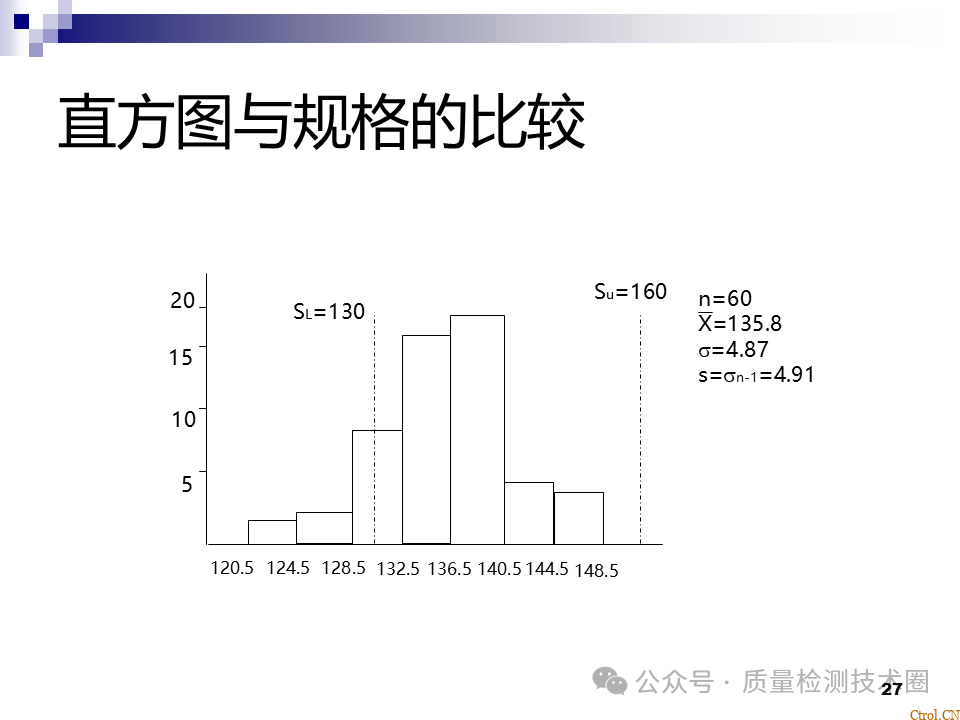
按频数表画出直方图。




























































正文完



![[转]内侧环形倒扣如何脱模?SQE你觉得这结构咋样](https://www.ctrol.cn/wp-content/themes/puock/timthumb.php?w=120&h=80&a=c&zc=1&q=90&src=https://www.ctrol.cn/wp-content/uploads/2017/09/020426W2w.jpg)








 多乐士
通过摸索发现ssh拉取会报错,直接网页访问下载会报404错误,不知道原因;但是可以通过群晖CM注册表访问下载,其方法如下:
Container Manager-注册表-设置-新增-注册表名称随便写,注册表URL填你的加速地址,勾选信任的SSL自我签署证书,登录信息不填-应用-使用你的地址,这是注册表会显示了,在搜索栏中输入映像名称,搜索结果在每一页的最后一个,你需要划到最后一个进行下载,实测可正常下载安装。
以上供网友参考。
多乐士
通过摸索发现ssh拉取会报错,直接网页访问下载会报404错误,不知道原因;但是可以通过群晖CM注册表访问下载,其方法如下:
Container Manager-注册表-设置-新增-注册表名称随便写,注册表URL填你的加速地址,勾选信任的SSL自我签署证书,登录信息不填-应用-使用你的地址,这是注册表会显示了,在搜索栏中输入映像名称,搜索结果在每一页的最后一个,你需要划到最后一个进行下载,实测可正常下载安装。
以上供网友参考。

