共计 2623 个字符，预计需要花费 7 分钟才能阅读完成。
SPC控制图有八种模式，即八种判断异常的检验准则，每一种检验准则代表一种异常现象，应用SPC控制图进行过程评估与监控，首先应掌握此八种检验模式，本文向您一一介绍SPC控制图的八种检验模式。
《常规控制图》国家标准GB/T4091——2001明确给出了变差的可查明原因的八种模式，如下图所示。这八种检验模式适用于均值图和单值图。假定质量特性X的观测值服从正态分布。上、下控制限分别位于中心线的上、下3σ距离处。为了便于应用这八种模式，将控制图分为6个区，每个区的宽度为1σ。6个区的标号为A、B、C、C、B、A，两个A区、B区、C区分别在中心线两侧，关于中心线对称。
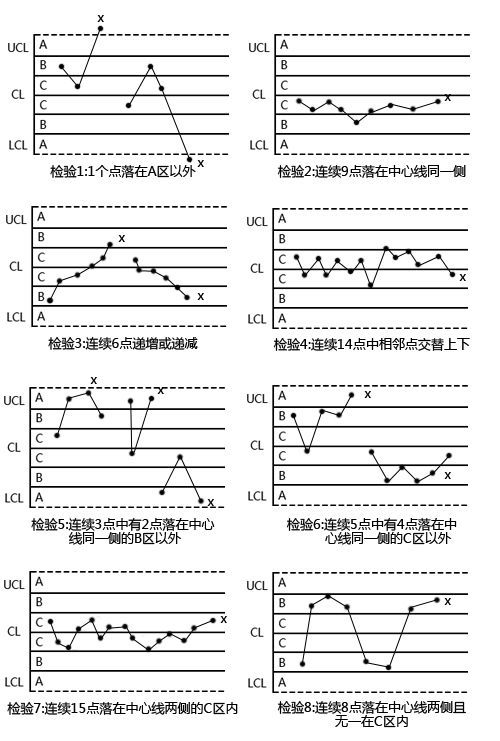
SPC控制图检验1：1个点落在A区以外
检验1给出了对控制图的基本解释：点出界就判异。当过程处于统计控制状态时，点子落在控制限内的概率为99.73%，落在控制限外的概率为1-99.73%=0.27%。检验1可以对过程中的单个失控做出反应，如计算、测量误差、原材料不合格、设备故障等。
SPC控制图检验2：连续9点落在中心线同一侧
当过程处于统计控制状态时，连续9点落在中心线同一侧的概率为P（连续9点落在中心线同一侧）=2*（0.5）9=0.003906=0.3906%即虚发报警的概率为0.3906%，第一类错误的概率为α=0.3906%。
在SPC控制图中心线同一侧连续出现的点成为链，链可能位于中心线的上测也可能位于中心线的下侧。注意：连必须由“连续”出现的点子构成。链中包含的点子数目成为链长。链长≥9，判断出现了异常。
“连续9点落在中心线同一侧”判断出现异常的一个重要原因是：模式2的α=0.3906%与“点出界就判异”的模式1的α=0.27%最接近。
出现检验2此种模式，主要是过程平均值减小的缘故。
SPC控制图检验3：连续6点递增或递减
当过程处于统计控制状态时，连续0.2733%，第一类错误的概率为α=0.2733%。
6点递增或递减的概率为P（连续6点递增或递减）=0.2733%即须发报警的概率为0.2733%
点子逐点上升或下降的状态称为倾向或趋势。注意，递减的下降倾向，后面的点子一定要低于或等于前面的点子，否则倾向中断，需要重新计算。递增的上升倾向也是同样的。
产生检验3模式的原因可能是工具逐渐磨损、维修逐渐变坏等，从而使得参数随着时间而变化。
SPC控制图检验4：连续14点中相邻点交替上下
“例如：两台设备、两只纺锤、两位操作工、两台自动售货机，它们交替使用所带来的系统影响会引发这样的现象。在记录交替倒置的鸡蛋计时器流出的沙子的时间时，也会观察到这样的现象，因此，这种模式又名‘鸡蛋计时器效应’。点子数的选择依据蒙特卡洛的试验结果，因为14点时虚发警报的概率（大约为0.004）与模式基本一致。”
SPC控制图检验5：连续3点中有2点落在中心线同一侧的B区以外
P（点子落在中心线一侧B区以外的概率）=P（X＞μ+2α）=1-P（X≤μ+2α）=1-0.9772=0.0228
P（连续3点中有2点落在中心线同一侧的B区以外）=6*0.02282* 0.9772=0.003048=0.3048%。
出现检验5模式的原因主要是由于过程参数μ发生了变化。
SPC控制图检验6：连续5点中有4点落在中心线同一侧的C区以外
当过程处于统计控制状态，连续5点中有4点落在中心线同一侧的C区以外的概率为：
P（点子落在中心线一侧C区以外的概率）= P（X＞μ+2α）=1-P（X≤μ+2α）=1-0.8413=0.1587
P（连续5点中有4点落在中心线同一侧的C区以外）=10*0.15874*0.8413= 0.005331=0.5331%即虚发报警的概率为0.5331%，第一类错误的概率为α=0.5331%。
检验6模式对于过程平均值的偏移也是较灵敏的。因此，出现此种模式的原因与检验5一样也是由于μ发生了变化。
SPC控制图检验7：连续15点落在中心线两侧的C区内
当过程处于统计控制状态时，连续15点落在中心线两侧的C区内的概率为：P（连续15点落在中心线两侧的c区内）=（1-0.1587*2）15=0.00326=0.326%即虚发报警的概率为0.326%，第一类错误的概率为α=0.326%。
对于“连续15点落在中心线两侧的C区内”这种模式在《常规控制图》国家标准GB/T4091——2001的参考文献中有这样一段描述：
“初学者往往认为这样的点子形式看上去很不错。然而，这种‘看上去不错’的点子形式依赖于所使用的缩放比例。所以，我们并不关心‘看上去’的情况，而是关注于这种点子形式所隐含的非随机性。蒙特卡洛试验结果确定以连续15点为模式7的临界值，因为15点的虚发警报的概率与模式1基本相等。模式7可用于检测分层问题。为了简化，假设子组大小为2，每个子组中的一个个体来自分布A，子组中的另一个个体来自分布B。如果分布A和分布B有不同的均值，那么，就使得基于极差的控制限间隔非常大。因此，并不是点子的变化不大，而是控制限太宽了。因此，应该注意：算法的错误是经常出现的，模式7所发出的警报原因是分层问题。”
SPC控制图检验8：连续8点落在中心线两侧且无一在的C区内
当过程处于统计控制状态时，连续8点落在中心线两侧且无一在C区内的概率为：P（连续8点落在中心线两侧且无一在C区内）=（0.1587*2）2=0.000103=0.0103%即虚发报警的概率为0.0103%，第一类错误的概率为α=0.0103%。
对于“连续8点落在中心线两侧且无一在C区内”这种模式在在《常规控制图》国家标准GB/T4091——2001的参考文献中有这样一段描述：
“如果考虑模式7描述的两个分布，假设子组中的数据要么来自分布A，要么来自分布B，而不是同时来自这两个分布，那么，就会出现模式8所显示的情况。”
