SPC控制图——3σ方式

共计 759 个字符，预计需要花费 2 分钟才能阅读完成。

上文中讲到SPC控制图的两种错误与解决办法，其解决办法就是调整上控制限与下控制限之间的距离，使其达到最优，而3σ就是接近这种最优间隔距离的方式。

   利用3σ方式构造SPC控制图的控制限为UCL=μ+3σ、CL=μ、LCL=μ-3σ，式中，μ、σ为统计量的总体参数。

   这是SPC控制图的总公式，具体应用时需要经过下列两个步骤：将3σ方式的公式具体化到所用的具体SPC控制图：对总体参数进行估计。

   应该注意：
   1、总体参数与样本参数不能混为一谈。对于生产的产品，其总体包括过去已经制成的产品、现在正在制造的产品以及未来将要制造的产品的全体。而样本只是过去已经制成产品的一部分，故总体参数的数值往往是不可能精确制导的，只能通过以往已知的数据来加以估计，而样本参数的数值则是可以获得的。

   2、规格界限不能用作控制限。规格界限是区分合格与不合格的科学界限，控制限则是区分偶波与异波的科学界限，二者完全是两码事，不能混为一谈。

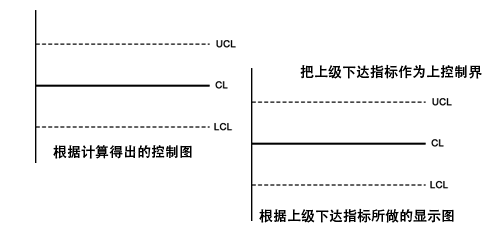
   例如：某邮局根据现场数据进行计算所得到的分拣差错率控制图如下图左侧图所示，但该邮局又把上级下达的分拣差错率指标作为UCL另搞了一张图，而且上级下达指标的数值恰巧与左侧控制图的CL水平相近。试分析：下图右侧图形是否还有控制图的作用？

   应用分布的观点分析如下：将左侧控制图稳态下的正态分布图形平移到右侧图中，立即可以看出，在生产正常的情况下，点子超出UCL的概率有50%之多，根本谈不上小概率事件，当然小概率事件原理也不可能发挥作用。故右图没有控制图的作用，而只是一张反映上级下达指标完成情况的显示图而已。

   经验证明，休哈特所提出的3σ方式是较好的，在多数情况下，3σ方式都接近上控制限与下控制限之间的最优间隔距离，从而使SPC控制图中不可避免的两种错误造成的总损失降到最低。