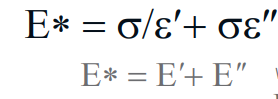共计 3266 个字符,预计需要花费 9 分钟才能阅读完成。
DMA测量材料对施加的振荡应力或应变的响应。要么控制施加的应力并记录样品中产生的应变,要么控制应变并测量产生的应力水平。
当一个应力被施加在聚合物系统上时,这个应力将在整个材料中消散,并且通常会导致某种程度的变形。聚合物本质上是粘弹性的。因此,当应力释放时,只有一部分变形是可逆的。这是响应的弹性部分。

σ =应力,ε=应变,κ =弹簧常数
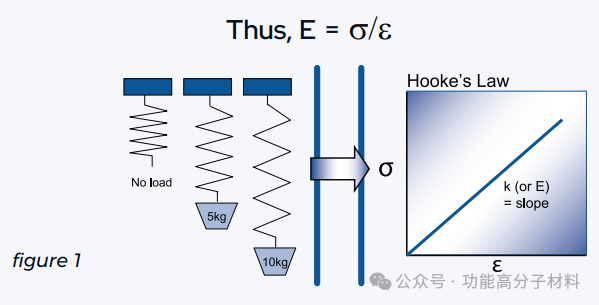
上面的等式表明,弹簧被拉伸的量与施加在它上面的应力量成正比。比例由弹簧常数k来描述。弹簧常数可以被认为是弹簧的刚度。另一个表示材料刚度的术语是模量E。

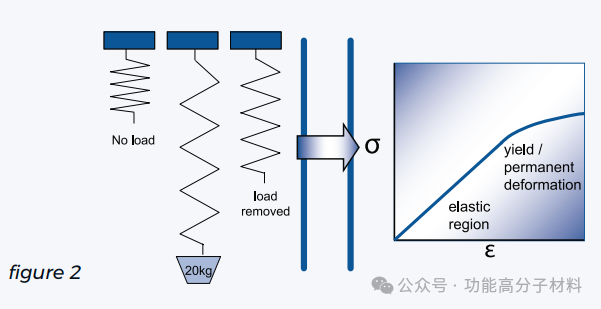
上面的图1显示了载荷与弹性弹簧伸长率之间线性关系的胡克定律。然而,如下图(图2)所示,如果载荷过大,弹簧实际上会发生一些永久性变形,在释放载荷后,弹簧将不再恢复到原来的长度。

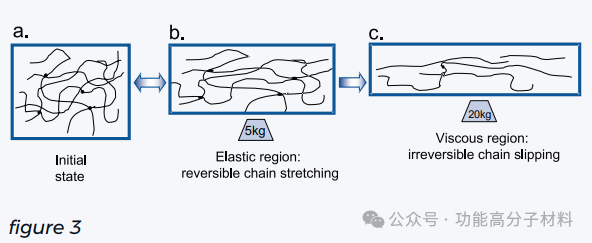
如下图3a和3b所示,当对聚合物系统施加非常低的应力水平时,卷曲的聚合物链将开始拉伸并略微伸直。这导致了低水平的变形。然而,就像弹簧一样,一旦负载被释放,熵将驱使大多数链反冲回它们原来的首选方向。
在更高的负载下,如图3c所示,分子链不仅会拉伸和展开,而且实际上会开始解开缠结并相互滑动。这种变形是不可逆转的。在极端情况下,分子链的滑动变得类似于粘性流动。如果系统不是交联的,材料最终会分开。然而,如果系统是交联的,它会拉伸和流动,直到交联成为唯一的力量把它结合在一起。最终,分子链会断裂,样品会失效。

胡克定律描述的是聚合物应力/应变行为的弹性成分,而理想流体的牛顿定律通常用于描述聚合物对应力黏性流动响应的另一个极端。

牛顿方程表明,理想流体在给定时间内的流量与施加在其上的应力成正比。比例是由流体的粘度来描述的。
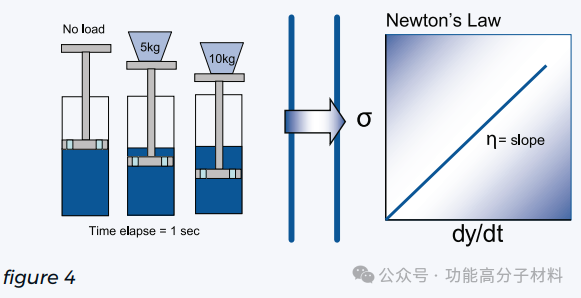
通常,汽车减震器被用来说明这种粘性流动行为。如图4所示,液体被迫通过气缸孔的速率取决于施加在减震器上的应力/载荷。与弹簧的可逆变形不同,阻尼器中流体的位移是完全不可逆的。因此,所有输入系统的功都消散在流体中。

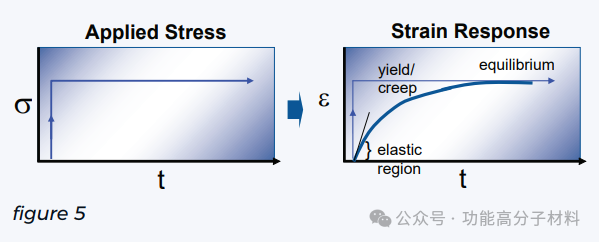
变形的粘性分量引入了时间作为一个关键变量。如前所述,聚合物首先会对施加的应力做出反应,通过拉伸和展开分子链,然后解开缠结,最后分子链相互滑动。这些聚合物重排需要时间才能发生。因此,随着时间的推移,聚合物对施加应力的实际响应看起来更像下图5:

如图所示,当对聚合物系统施加恒定的应力或载荷时,第一反应是弹性链拉伸/解卷,导致弹性变形。如果聚合物是一个真正的弹簧,变形将很快达到一个平衡点,不会发生额外的变形(就像挂在弹簧末端的重物)。然而,对于粘弹性系统,持续的载荷将导致聚合物链开始解开并滑动。解开缠结的过程也将允许聚合物线圈多拉伸一点。随着时间的推移,这种滑动和额外的拉伸导致额外的变形,称为蠕变。最终,分子链将被拉伸到它们所能达到的极限,进一步的变形将来自于任何非交联链的纯粘性链滑移。
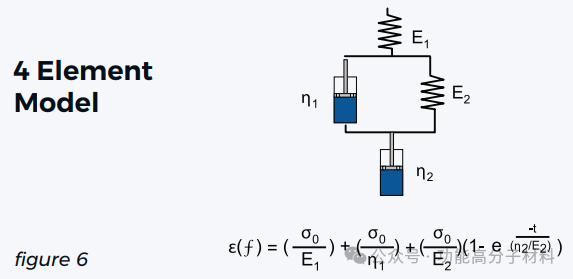
许多力学模型被开发出来模拟粘弹性行为。其中最流行的是图6所示的4元素模型。第一个弹簧控制初始弹性响应,然后是弹簧和阻尼器元件并联的混合区域,最后是纯粘性阻尼器元件与上述所有元件串联。

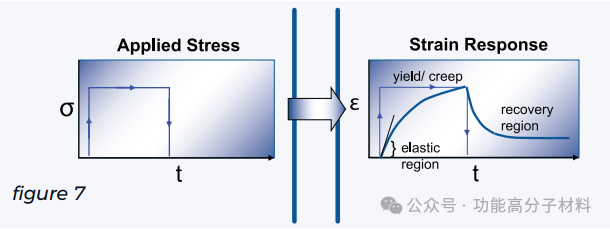
当应力/负载被释放时,熵将缓慢地使拉伸的聚合物链卷曲回其原始状态。然而,只有变形的弹性部分会被恢复,并且样品相对于其初始状态将保持一定的变形(图7)。

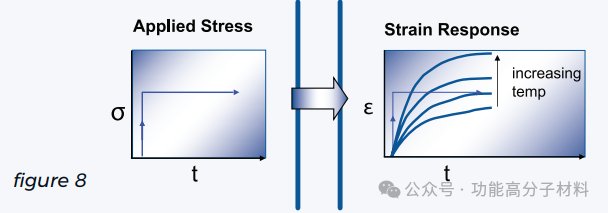
影响材料应力/应变行为的最后一个关键因素是温度。如图8所示,温度越高,聚合物链的迁移率越高。这导致在给定载荷下比在较低温度下测试相同材料时更快更大的变形。

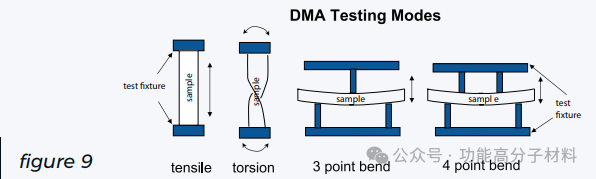
动态力学分析通常测量材料对振荡外加应力的应变响应。在某些情况下,可以控制施加的应变,并测量材料中产生的应力水平,但这种情况不太常见。图9显示了DMA的一些可能的测试几何形状。

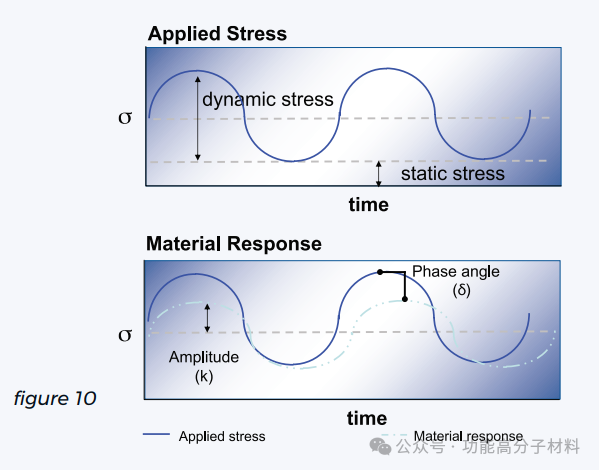
无论何种形式的应力(拉伸、扭转或弯曲)施加到样品上,所有的DMA都会对给定样品施加正弦应力或应变,并测量由此产生的材料响应。


σ=在给定时间的应力, =最大施加应力,ω=振荡的频率
=最大施加应力,ω=振荡的频率
材料的响应将取决于它的相对程度的弹性和粘性的特性。越有弹性的材料,更接近的响应将跟踪应用应力剖面。然而,材料越粘稠,其流动和响应施加载荷所需的时间就越长,变形的可逆性就越小。因此,图10所示材料的应变响应与外加应力的相偏差为δ:


该表达式表明,应变实际上是由两个90˚相外的项组成的。上面的方程可以用实分量和虚分量的贡献来表示:

第一项包含实分量。这代表了应变响应的一部分,这是由于材料的弹性性质。第二项是响应的非相位部分,它反映了材料通过粘性机制耗散能量的能力。材料的复模量可以用应力方程除以应变方程来计算:

Ε’ =实数或“储存”模量,Ε″=虚模或“损失”模量

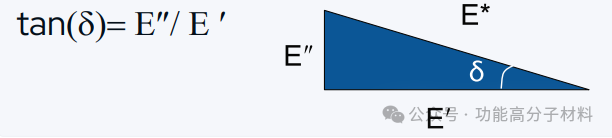
tan(δ)是一个有意义的性质,因为它表示在给定条件下材料的粘性与弹性贡献的比率。
虽然室温下储存模量和损耗模量的绝对值和相对值都是有价值的,但通常DMA是作为温度的函数运行的。在很宽的温度范围内测量材料对振荡应力的响应可以提供大量关于热转变的信息。例如,DMA提供了测量材料Tg的最高分辨率技术之一。

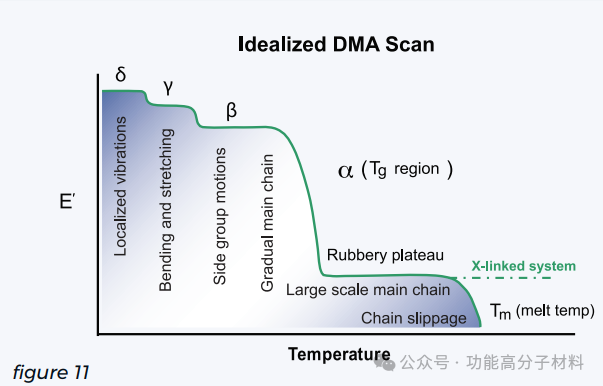
图11中理想化的DMA曲线显示了材料的储存模量随温度的变化,能够揭示其热转变的大量信息。最常报道的热固性聚合物的热转变是它的玻璃化转变温度(Tg)。如前所述,材料的Tg实际上并不是一个离散的热力学转变,而是一个温度区域,在这个温度区域上,聚合物链的迁移率显著增加,材料从刚性、玻璃态转变为更具橡胶性/柔顺性的状态。当材料响应从主要的弹性/可逆变形转变为越来越多的粘性/不可逆链式运动时,储存模量的显著下降表明了这种变化。这个大的转变,α转变(α),通常是Tg的来源。在玻璃化过渡区之外是“橡胶”区域,其中弹性与粘性贡献的比例达到平衡。对于交联热固性材料,这个平台一直保持到达到降解温度。对于非交联体系,熔体温度最终将达到,并导致类似液体的流动。
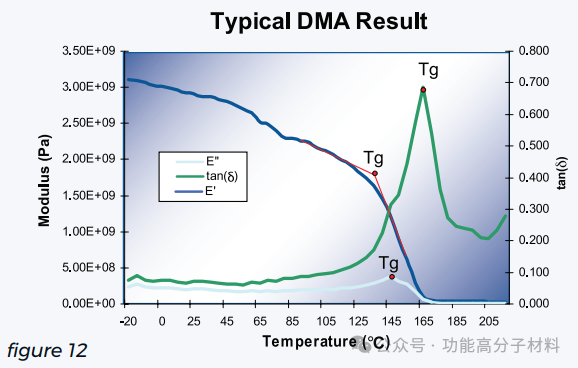
图12显示了环氧树脂的典型DMA图的示例。该图显示了储存模量和损耗模量以及tan(δ)。从这个图中,Tg区域可以从几个方面看到。计算Tg的第一种方法是从储存模量(E ‘)曲线下降的开始。这表示粘性运动开始起作用的点。第二种方法是损耗模量(E″)曲线的峰值。这表示交联系统中链滑移最大的点。最后,可以用tan(δ)曲线的峰值来确定Tg。这表示黏性响应与弹性响应之比最大的点。

tan(δ)曲线的峰值是Tg的一个常用测量点,因为它通常比确定储存模量下降的开始更容易分离。然而,这个案例再次强调了一个事实,即确定如何测量Tg是很重要的,因为这三种确定Tg的方法在行业中都是公认的,但会给出不同的绝对值。由tan(δ)峰计算的Tg总是高于由储存模量计算的Tg。通常,由损耗模量计算的Tg会落在两者之间。
tan(δ)随温度的变化曲线可以用来确定一个系统的更多信息,而不仅仅是Tg。tan(δ)峰的宽度可以表示一个体系的均匀程度。具有非常宽峰的体系通常由不同聚合物链长度或结构的混合物组成,从而产生更宽的温度范围,从而为各种组分发起显著的粘性链运动。另一方面,峰窄的体系通常链型和分子量分布更窄。
tan(δ)曲线的高度或振幅与材料通过链段运动耗散能量的能力直接相关。具有高tan(δ)峰的系统具有更高的吸能粘度运动比,因此通常比具有低tan(δ)振幅的系统更坚固。
DMA曲线数据的最后一个常见用途是最基本的——确定材料在给定温度下的模量。由于模量测量材料的刚度,因此通常将其与材料的CTE知识结合使用,以确定粘合基板在热应力期间可能发生的应力水平。
降低热循环过程中粘结应力的最佳方法是使胶粘剂的热膨胀特性与基材的热膨胀特性相匹配。不幸的是,这并不总是可能的。下一个最佳选择可能是选择具有较低模量或较高韧性的材料,可以吸收热膨胀不匹配引起的任何应力。
对于这些计算,我们通常使用储存模量,因为我们假设粘合线上的变形很可能足够小,以使粘合剂保持在其弹性极限内。


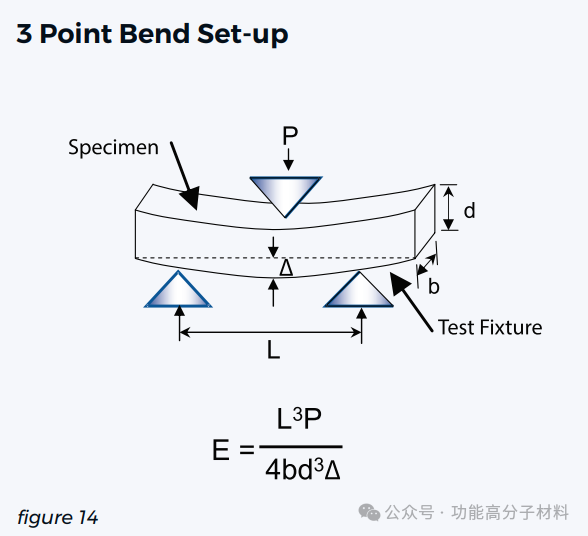
图14显示了用于测量模量的样品几何形状。在三点弯曲中测试一个小的,3.0mm x 1.0mm x 18.0mm的材料棒。

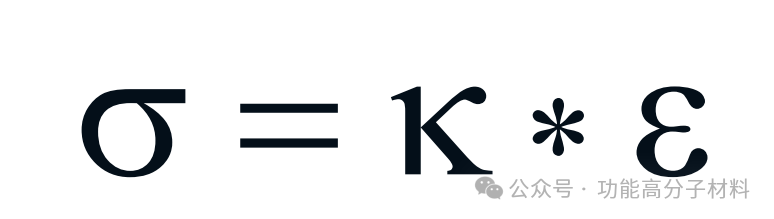
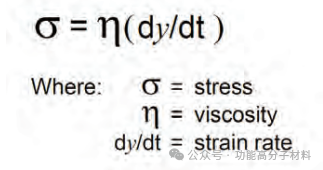
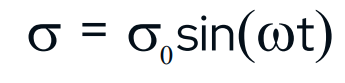
![]() =最大施加应力,ω=振荡的频率
=最大施加应力,ω=振荡的频率![]()
![]()
![]()
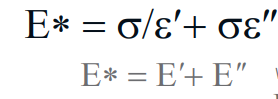

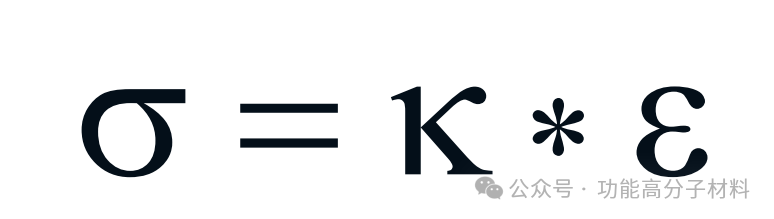



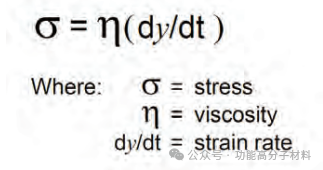







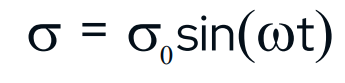
![]() =最大施加应力,ω=振荡的频率
=最大施加应力,ω=振荡的频率![]()
![]()
![]()